XLXZ's Blog

安装完python之后，我们需要配置python的环境变量，使用非 windows 自带的 store 里面的 python 的话，在调用 python 指令的时候，会优先打开应用商店并推荐下载里面的python，但是实际上我们已经安装了python，所以我们需要配置环境变量。下面是配置环境变量的步骤：

1. 找到python的安装路径。

一般是在 C:\Users\用户名\AppData\Local\Programs\Python\Python版本号 下面，在cmd中使用 where python 可以查看python的安装路径。

我这里使用的是 anaconda ，我将其安装在了 E:\Anaconda 下面,版本为3.11。

另外，你可以发现，在 C:\Users\用户名\AppData\Local\Micosoft\WindowsApps 下面也有一个python的路径，但是这个路径是一个快捷方式，不是真正的python的安装路径。这个快捷方式指向的是 store 里面的 python。他会打开store里面的安装界面，推荐你下载store里面的python……而且系统默认环境变量的python也是这个路径，就很无语……

可以通过 python --version 查看python的版本，你看，如果查看那个快捷方式的python的版本，它不会显示版本号：

安装 torch,d2l 以及其他的必要库

接下来我们需要安装 torch 和 d2l 以及其他的必要库。找到安装的anaconde 的 Anaconda Prompt，在里面输入以下指令：

1 2	pip install torch torchvision torchaudio pip install d2l

这样就安装好了 torch 和 d2l 了。

你可以使用 pip list 查看已经安装的库。

另外，使用 pip 安装和使用 conda 安装有一点点区别，conda 安装的库会放在 E:\Anaconda\envs\你的环境\Lib\site-packages 下面，而 pip 安装的库会放在 E:\Anaconda\Lib\site-packages 下面。除非是你需要打包你的软件，否则的话两个实际上都是一样的。

在这里挖一个坑，后面再填：[[pip和conda的区别]]

juoyter notebook 的安装和配置

jupyter notebook 包含了记笔记和运行代码的功能，你可以在查看教程的同时，运行里面镶嵌的代码，并且根据自己的理解修改代码，尝试不同的运行结果，这样可以更好的理解代码的含义。

首先，我们将 D2L Notebooks 的代码下载到本地：

mkdir d2l-zh && cd d2l-zh
curl https://zh-v2.d2l.ai/d2l-zh-2.0.0.zip -o d2l-zh.zip
unzip d2l-zh.zip && rm d2l-zh.zip
cd pytorch

然后，我们需要安装 jupyter notebook，使用以下指令：

1	pip install jupyter

这个库实际上 anaconda 里面已经自带了，但是它不在环境变量里面，我们需要将其添加到环境变量，这样才能够直接执行 jupyter notebook 这个指令。

这里建议使用 everything 这个工具，可以很方便的查找文件，输入 jupyter 就可以找到 junpyter 这个程序的位置，然后将其添加到环境变量即可。

然后，我们就可以使用在 D2L 的文件夹目录下执行 jupyter notebook 来打开 jupyter notebook 了。

d2l-1-基础知识和数据处理

发表于 2024-07-30 更新于 2024-08-01 本文字数： 1.3k 阅读时长 ≈ 5 分钟

# python
# d2l

基础知识——符号说明

实际上，学习深度学习，对于初学者来说，需要的基础知识面很广，比如说微积分，概率论，线性代数等，但是实际上涉及的并不深…

上面的东西刚好大一就会学，所以说，对于大一的同学来说，学习这个东西基本上没有障碍……简单回顾一下下面的这些数学符号基本上就差不多了：

本书中使用的符号概述如下。 ### 数字

\(x\)：标量
\(\mathbf{x}\)：向量
\(\mathbf{X}\)：矩阵
\(\mathsf{X}\)：张量
\(\mathbf{I}\)：单位矩阵
\(x_i\), \([\mathbf{x}]_i\)：向量\(\mathbf{x}\)第\(i\)个元素
\(x_{ij}\), \([\mathbf{X}]_{ij}\)：矩阵\(\mathbf{X}\)第\(i\)行第\(j\)列的元素

集合论

\(\mathcal{X}\): 集合
\(\mathbb{Z}\): 整数集合
\(\mathbb{R}\): 实数集合
\(\mathbb{R}^n\): \(n\)维实数向量集合
\(\mathbb{R}^{a\times b}\): 包含\(a\)行和\(b\)列的实数矩阵集合
\(\mathcal{A}\cup\mathcal{B}\): 集合\(\mathcal{A}\)和\(\mathcal{B}\)的并集
\(\mathcal{A}\cap\mathcal{B}\)：集合\(\mathcal{A}\)和\(\mathcal{B}\)的交集
\(\mathcal{A}\setminus\mathcal{B}\)：集合\(\mathcal{A}\)与集合\(\mathcal{B}\)相减，\(\mathcal{B}\)关于\(\mathcal{A}\)的相对补集

函数和运算符

\(f(\cdot)\)：函数
\(\log(\cdot)\)：自然对数
\(\exp(\cdot)\): 指数函数
\(\mathbf{1}_\mathcal{X}\): 指示函数
\(\mathbf{(\cdot)}^\top\): 向量或矩阵的转置
\(\mathbf{X}^{-1}\): 矩阵的逆
\(\odot\): 按元素相乘
\([\cdot, \cdot]\)：连结
\(\lvert \mathcal{X} \rvert\)：集合的基数
\(\|\cdot\|_p\): ：\(L_p\) 正则
\(\|\cdot\|\): \(L_2\) 正则
\(\langle \mathbf{x}, \mathbf{y} \rangle\)：向量\(\mathbf{x}\)和\(\mathbf{y}\)的点积
\(\sum\): 连加
\(\prod\): 连乘
\(\stackrel{\mathrm{def}}{=}\)：定义

微积分

\(\frac{dy}{dx}\)：\(y\)关于\(x\)的导数
\(\frac{\partial y}{\partial x}\)：\(y\)关于\(x\)的偏导数
\(\nabla_{\mathbf{x}} y\)：\(y\)关于\(\mathbf{x}\)的梯度
\(\int_a^b f(x) \;dx\): \(f\)在\(a\)到\(b\)区间上关于\(x\)的定积分
\(\int f(x) \;dx\): \(f\)关于\(x\)的不定积分

概率与信息论

\(P(\cdot)\)：概率分布
\(z \sim P\): 随机变量\(z\)具有概率分布\(P\)
\(P(X \mid Y)\)：\(X\mid Y\)的条件概率
\(p(x)\): 概率密度函数
\({E}_{x} [f(x)]\): 函数\(f\)对\(x\)的数学期望
\(X \perp Y\): 随机变量\(X\)和\(Y\)是独立的
\(X \perp Y \mid Z\): 随机变量\(X\)和\(Y\)在给定随机变量\(Z\)的条件下是独立的
\(\mathrm{Var}(X)\): 随机变量\(X\)的方差
\(\sigma_X\): 随机变量\(X\)的标准差
\(\mathrm{Cov}(X, Y)\): 随机变量\(X\)和\(Y\)的协方差
\(\rho(X, Y)\): 随机变量\(X\)和\(Y\)的相关性
\(H(X)\): 随机变量\(X\)的熵
\(D_{\mathrm{KL}}(P\|Q)\): \(P\)和\(Q\)的KL-散度

复杂度

\(\mathcal{O}\)：大O标记

数据处理

数据处理主要涉及到两个核心的问题，一个是如何读取数据，另外一个则是如何处理为空的数据。

将数据处理之后我们还需要将其转换为

读取数据

在Python中，我们可以使用pandas库来读取数据，pandas库提供了read_csv函数，可以读取csv文件，返回一个DataFrame对象。

作为实例，我们创建一个人工数据集，然后将其保存为csv文件，然后使用pandas库读取数据。

import os

os.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:
    f.write('NumRooms,Alley,Price\n')  # 列名
    f.write('NA,Pave,127500\n')  # 每行表示一个数据样本
    f.write('2,NA,106000\n')
    f.write('4,NA,178100\n')
    f.write('NA,NA,140000\n')

import pandas as pd
data = pd.read_csv(data_file)
print(data)

处理空数据

在panda中，数据集中的空数据被标记为NA，在进行机器训练的时候，不能让机器直接处理空数据，所以说我们需要对空数据进行处理，一般有下述几种办法: 1. 删除法 2. 插值法

删除法将带有空数据的行视为无效数据，直接删除，插值法则是用已知数据的平均值或者中位数等来填充空数据。

在这里，我们用插值法来处理空数据。

# 读取输入和输出数据
inputs = data.iloc[:, [0,1]]
outputs = data.iloc[:, 2]

# 用平均值填充空数据
tempRaw = data.iloc[:,0]
print(tempRaw,tempRaw.mean())
tempRaw = tempRaw.fillna(tempRaw.mean())
print(tempRaw,type(tempRaw))

print(inputs,type(inputs))
inputs.iloc[:, 0] = tempRaw
print(inputs)
print(outputs)

下面逐行解释一下上述代码：

[[data.iloc]] 用于选取数据集中的行和列，data.iloc[:, [0,1]]表示选取所有行和第0、1列的数据，data.iloc[:, 2]表示选取所有行和第2列的数据。

[[data.fillna]] 用于填充空数据，tempRaw.fillna(tempRaw.mean())表示用该列的平均值填充空数据。

[[data.iloc]] 返回的是一个DataFrame对象，我们可以直接对其进行操作，inputs.iloc[:, 0] = tempRaw表示将tempRaw的数据赋值给inputs的第0列。

转换为张量

使用 pandas 读取数据之后，我们得到的数据类型是 pandas 的 DataFrame 对象，我们需要将其转换为张量，才能用于训练。

import torch

X = torch.tensor(inputs.to_numpy(dtype=float))
y = torch.tensor(outputs.to_numpy(dtype=float))
X, y

torch.tensor() 使用 numpy 数组初始化创建一个张量，inputs.to_numpy() 将 DataFrame 对象转换为 numpy 数组，dtype=float 表示将数据转换为浮点数类型。

数据从 DataFrame -> numpy 数组 -> 张量，完成了数据的转换。

d2l-3-softmax回归

发表于 2024-07-30 更新于 2024-08-02 本文字数： 721 阅读时长 ≈ 3 分钟

# d2l
# python

对于一般模型的概述

在深度学习中，实际上对于任意的一个模型，都有两个重要的部分： 1. 模型的结构 2. 模型的损失函数

模型的结构定义了模型的计算过程，而损失函数定义了模型的优劣并且指导模型的优化。

softmax回归

线性回归用于解决回归问题，softmax回归用于解决分类问题。

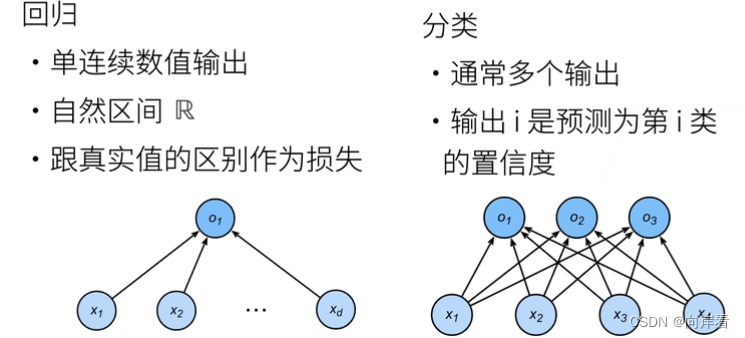
在简单的线性回归中，我们期望模型能够输出一个标量值，对于一系列输入而言，其能够输出符合预期的结果。

softmax 回归也类似，其被用于解决分类问题，我们希望模型能够输出一个n维向量，这个向量的每一个元素代表了输入属于某个类别的概率。

softmax 函数

为了达到这样的目的，我们需要引入 softmax 函数，其能够将模型的输出转换为概率。softmax 函数的定义如下： \[softmax(x)_i = \frac{exp(x_i)}{\sum_{j=1}^{n}exp(x_j)}\]

其中，\(x\) 为模型的输出，\(n\) 为类别的数量，\(softmax(x)_i\) 代表了输入属于第 \(i\) 个类别的概率。这个函数的优点在于，其能够保持输出的概率和为1，并且各个概率值都在0到1之间。另外，由于 \(exp(x)\) 是一个非线性函数，因此 softmax 函数也是一个非线性函数，这使得模型对于较大的输入值更加敏感，从而能够更好地区分不同的类别。

损失函数——交叉熵

soft函数很好的解决了从模型的输出到概率的转换问题，

但是这样也引出来了另一个问题，为了优化参数，我们需要定义一个损失函数，但是对于分类问题，我该如何定义损失函数呢？这里我们引入了交叉熵损失函数，其定义如下：

\[H(y, \hat{y}) = -\sum_{i=1}^{n}y_i\log(\hat{y}_i)\]

其中，\(y\) 为真实的标签，\(\hat{y}\) 为模型的输出，\(n\) 为类别的数量。

这个损失函数的优点在于，其能够衡量模型的输出与真实标签之间的差距，当模型的输出与真实标签完全一致时，交叉熵损失函数的值为0，当模型的输出与真实标签差距越大时，交叉熵损失函数的值也越大。

对于分类问题，我们期望的输出应当是除了真实标签之外，其他标签的概率都应该接近于0，而真实标签的概率应该接近于1。通过计算交叉熵损失函数，我们就能够衡量模型的输出与真实标签之间的差距，从而指导模型的优化。

d2l-2-线性回归的简单实现

发表于 2024-07-30 更新于 2024-08-02 本文字数： 759 阅读时长 ≈ 3 分钟

# python
# d2l

在神经网络中，训练的本质实际上是优化参数，使得模型的预测值与真实值之间的误差尽可能小。通过定义损失函数的方式，我们可以知道参数与结果之间的关系，通过求导的方式，我们可以知道如何调整参数使得损失函数最小。

假设损失函数为 \(L(\theta)\)，那么我们的目标就是找到一个 \(\theta\) 使得 \(L(\theta)\) 最小。对于一个给定的 \(\theta\)，我们可以通过计算 \(L(\theta)\) 得知其的损失，然后我们求导 \(L(\theta)\)，得到其在 \(\theta\) 处的梯度 \(\nabla L(\theta)\)，然后我们可以通过梯度下降的方式，即 \(\theta = \theta - \alpha \nabla L(\theta)\) 来更新 \(\theta\) 。其中 \(\alpha\) 是学习率，是一个超参数，用来控制每次更新的步长。

上述的方法即为梯度下降法，是一种常用的优化方法。从数学上可以证明，梯度下降最终一定能找到一个局部最优解。

在实际运用的时候，我们经常将多个样本的损失函数的平均值作为最终的损失函数，即 \(L(\theta) = \frac{1}{n} \sum_{i=1}^{n} L(\theta, x_i, y_i)\)，其中 \(n\) 为样本的数量，\(x_i\) 为第 \(i\) 个样本的特征，\(y_i\) 为第 \(i\) 个样本的标签。但是这样又引出了另一个问题，即当样本数量很大的时候，我们需要计算所有样本的梯度，这样会导致计算量过大，因此我们通常会采用随机梯度下降法，即每次只计算随机选择的多个样本，然后更新参数，而不是全部样本。

下面，我们生成一个人工数据集，然后使用梯度下降法来拟合这个数据集。

import torch
import numpy as np
import random
import matplotlib.pyplot as plt

# 生成数据集
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.tensor(np.random.normal(0, 1, (num_examples, num_inputs)), dtype=torch.float)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
# 加入噪声
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)

# 读取数据
def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)])
        yield features.index_select(0, j), labels.index_select(0, j)

batch_size = 10
for X, y in data_iter(batch_size, features, labels):
    print(X, y)
    break

接下来，我们定义模型和损失函数。

# 定义模型，这里我们不使用 nn.Module，而是自己手搓
def linreg(X, w, b):
    """线性回归模型。"""
    return torch.matmul(X, w) + b

# 定义损失函数
def loss(y_hat, y):
    """均方损失。"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

# 定义优化算法
def sgd(params, lr, batch_size):  #@save
    """小批量随机梯度下降。"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

# 初始化参数
w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float, requires_grad=True)
b = torch.zeros(1, dtype=torch.float, requires_grad=True)

# 训练模型
lr = 0.03
num_epochs = 3
net = linreg
loss = loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y).sum()
        l.backward()
        sgd([w, b], lr, batch_size)
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')