d2l-3-softmax回归
对于一般模型的概述
在深度学习中,实际上对于任意的一个模型,都有两个重要的部分: 1. 模型的结构 2. 模型的损失函数
模型的结构定义了模型的计算过程,而损失函数定义了模型的优劣并且指导模型的优化。
softmax回归
线性回归用于解决回归问题,softmax回归用于解决分类问题。
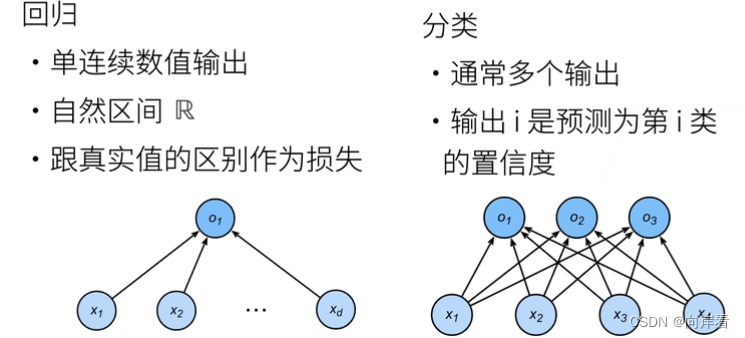
在简单的线性回归中,我们期望模型能够输出一个 标量值,对于 一系列 输入而言,其能够输出符合预期的结果。
softmax 回归也类似,其被用于解决分类问题,我们希望模型能够输出一个n维向量,这个向量的每一个元素代表了输入属于某个类别的概率。
softmax 函数
为了达到这样的目的,我们需要引入 softmax 函数,其能够将模型的输出转换为概率。softmax 函数的定义如下: \[softmax(x)_i = \frac{exp(x_i)}{\sum_{j=1}^{n}exp(x_j)}\]
其中,\(x\) 为模型的输出,\(n\) 为类别的数量,\(softmax(x)_i\) 代表了输入属于第 \(i\) 个类别的概率。这个函数的优点在于,其能够保持输出的概率和为1,并且各个概率值都在0到1之间。另外,由于 \(exp(x)\) 是一个非线性函数,因此 softmax 函数也是一个非线性函数,这使得模型对于较大的输入值更加敏感,从而能够更好地区分不同的类别。
损失函数——交叉熵
soft函数很好的解决了从模型的输出到概率的转换问题,
但是这样也引出来了另一个问题,为了优化参数,我们需要定义一个损失函数,但是对于分类问题,我该如何定义损失函数呢?这里我们引入了交叉熵损失函数,其定义如下:
\[H(y, \hat{y}) = -\sum_{i=1}^{n}y_i\log(\hat{y}_i)\]
其中,\(y\) 为真实的标签,\(\hat{y}\) 为模型的输出,\(n\) 为类别的数量。
这个损失函数的优点在于,其能够衡量模型的输出与真实标签之间的差距,当模型的输出与真实标签完全一致时,交叉熵损失函数的值为0,当模型的输出与真实标签差距越大时,交叉熵损失函数的值也越大。
对于分类问题,我们期望的输出 应当是 除了真实标签之外,其他标签的概率都应该接近于0,而真实标签的概率应该接近于1。通过计算交叉熵损失函数,我们就能够衡量模型的输出与真实标签之间的差距,从而指导模型的优化。
