微积分下:第一周课程记录
在这里简单的回顾一下第一周微积分都学了些什么~
矢量的计算
首先就是温习了一下矢量的计算规则,包括 [点乘] 和 [叉乘]
点乘
挺简单的不再赘述,基本的运算法则。基本的计算形式就是:(a,b)·(c,d) = ac+db
叉乘
叉乘的方向
叉乘的方向与原来的两个向量垂直,在用于计算比如说面的特征向量,或者求与直线垂直的向量的时候十分的方便。
叉乘的大小
叉乘的计算公式是:
数值上和方向上都是一致的,其中ijk为基向量。
几何意义
实际上等效于AB夹出来的那个平行四边形的面积
点乘叉乘混合运算
计算技巧:转化为矩阵计算
然后很多计算用矩阵的角度就很容易计算了
几何意义
实际上 大小 等于 ABC张出来的四棱柱 的体积
线面的计算
面
面的几种表示方式:
- 点法式:
法 向 量 。 - 一般式:Ax+By+Cz+D=0
- 截距式:
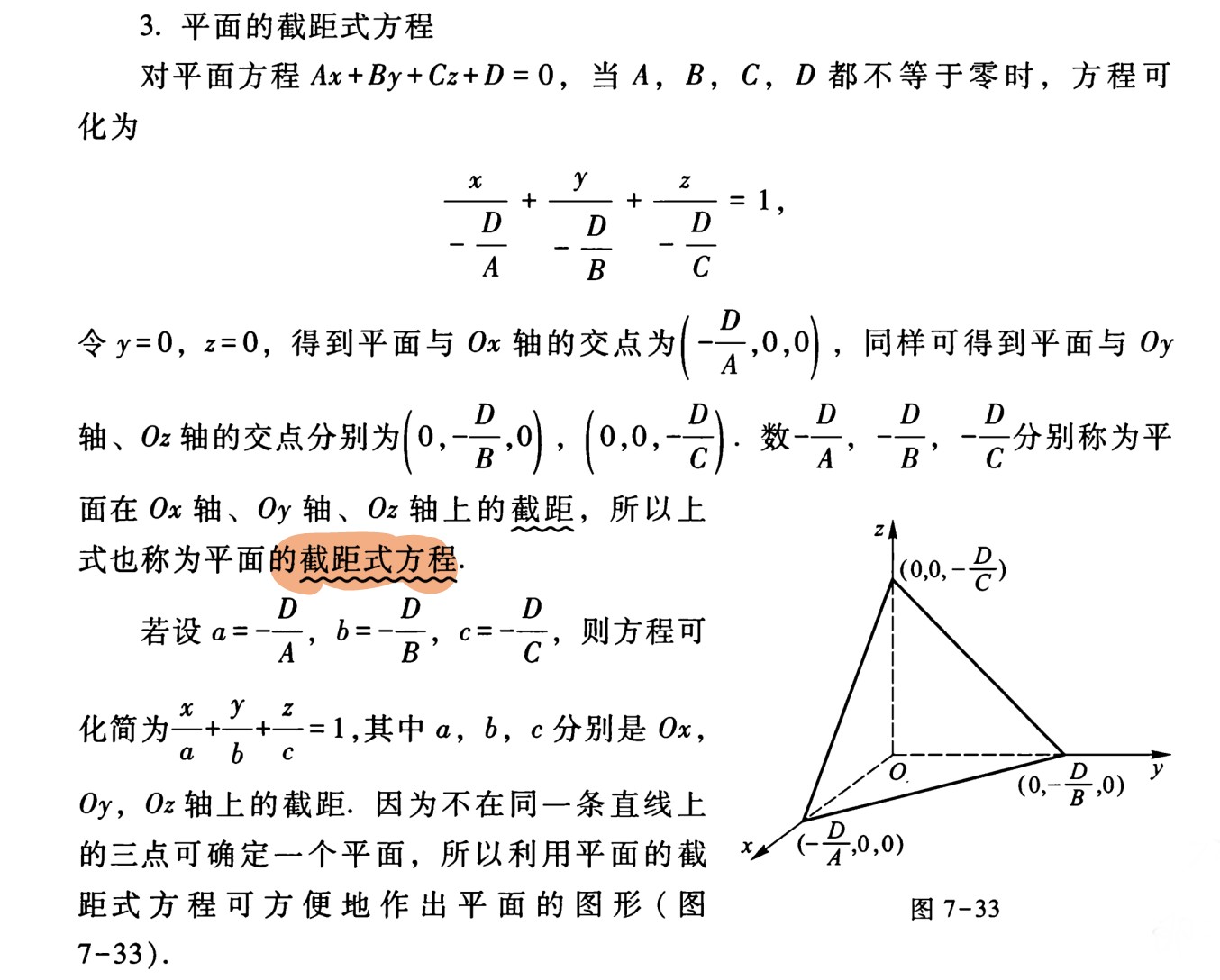
平行面之间的距离
点到平面的距离
线
线的几种表示方式
标准方程/点向式:

参数式:
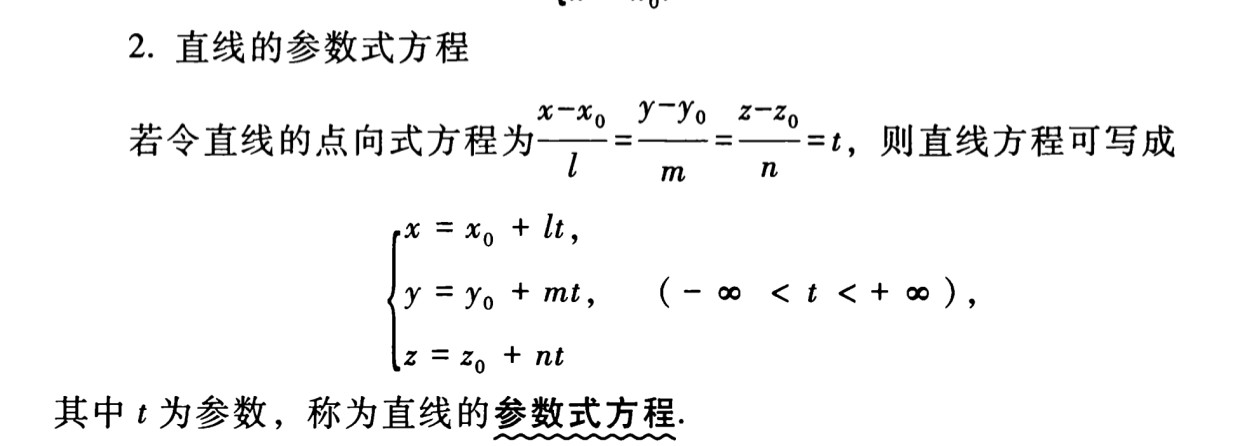
一般式(使用两面相交表示)
一般式求方向向量
求两个面的法向量,然后将他们叉乘,L属于面A和B,就必然同时垂直于A、B的法向量。
点到线的距离
通过构造 过点P 且 与线垂直 的面,求得Q点为面与线的交点,此时PQ即为点到线的距离。
Q点可可以通过将直线转化为参数式计算出参数t大小,然后带入会方便一点。
