2023-12-3数模讲座记录（海底测线）
一、题目描述
1 | title: 国赛2023-B题 |
二、问题解决
1.前面两道问题
其实就是纯数学问题
总的来说不是特别难，只需要使用三角函数即可。 #### 定义： - 坡度 ：\(\alpha\) - 波束的覆盖宽度：W - 相邻两条带间重叠率：η - 换能器开角：θ - 水深：D - 相邻测线间距：d - 海底坡度：αη=1-dW - （测线方向与海底坡面法向在水平面上投影的夹角β）
解答：
第一题：根据正弦定理，当水深为D时，测线的宽度：
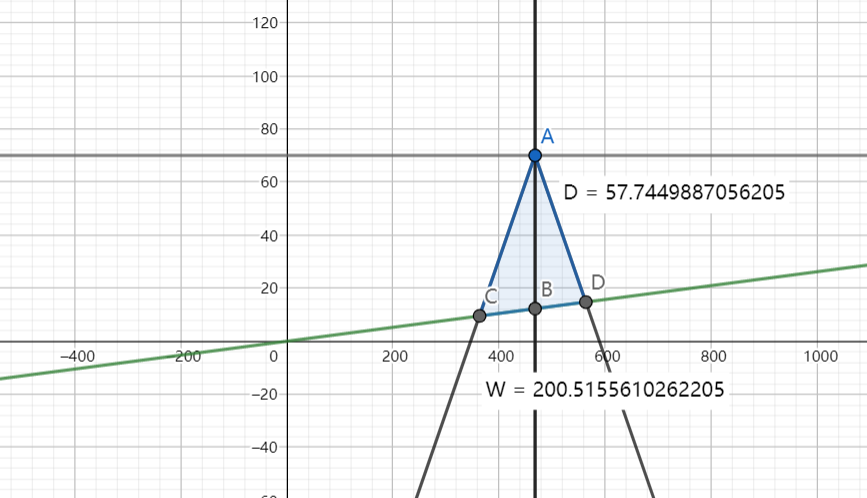
\[W=\frac{D\sin{\frac{\theta}{2}}}{\sin{(\frac{\pi-\theta}{2}-\alpha)}}+\frac{D\sin{\frac{\theta}{2}}}{\sin{(\frac{\pi-\theta}{2}+\alpha)}}\]
第二题：如图，设图中标注线段长为X
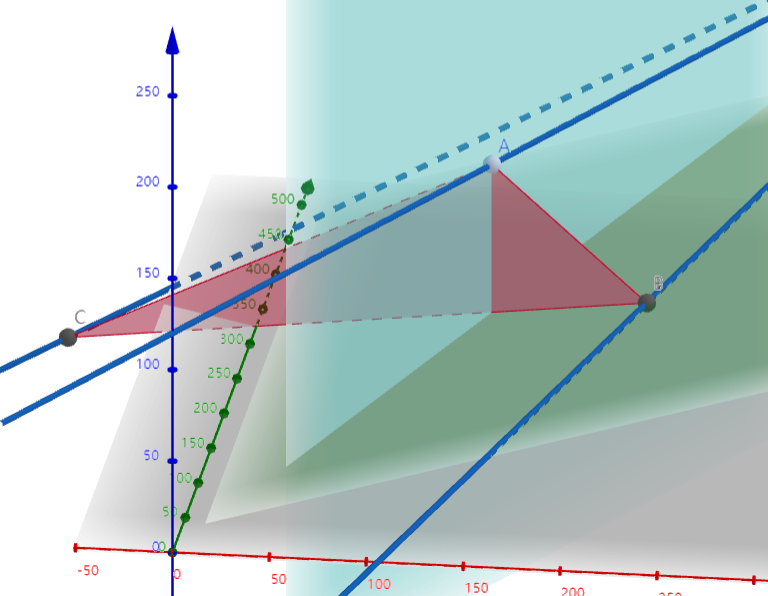
\[ \tan \gamma = \frac{X\tan \alpha }{\frac{X}{\sin (\pi -\beta )} } =\tan \alpha \sin (\pi -\alpha ) \]
化简得到：
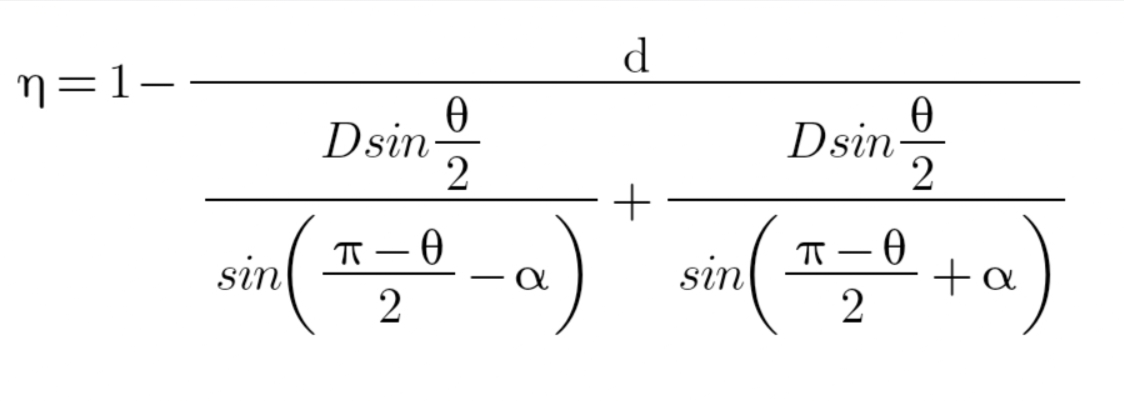
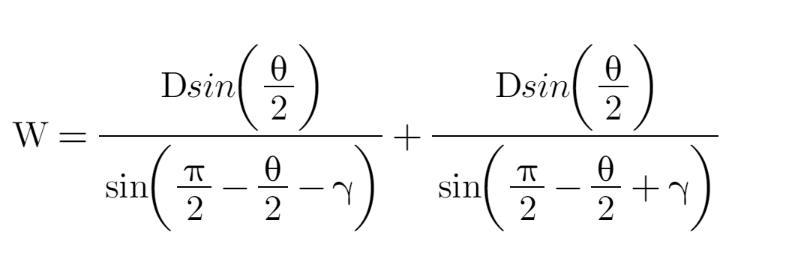
可视化之后如下：
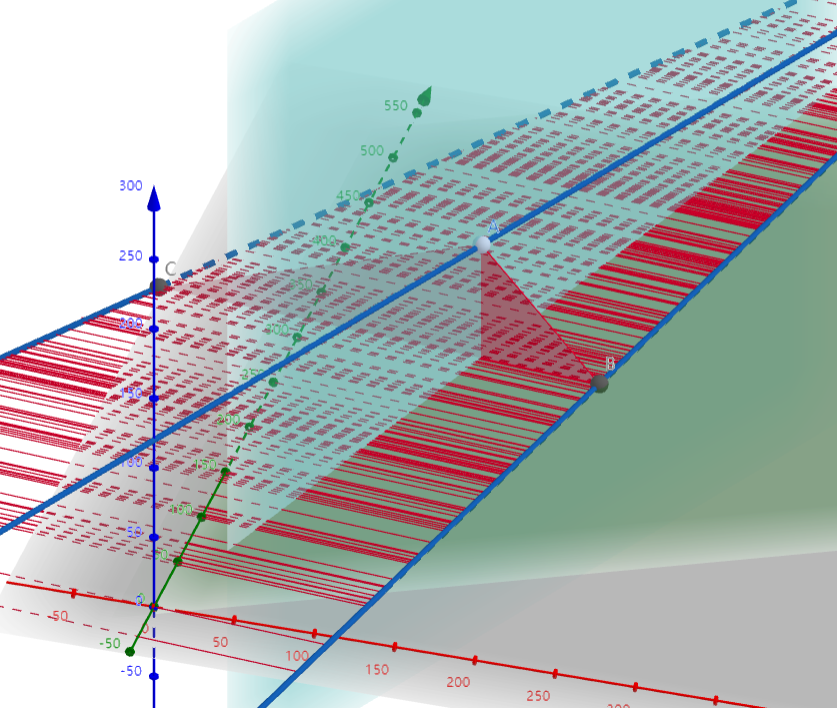
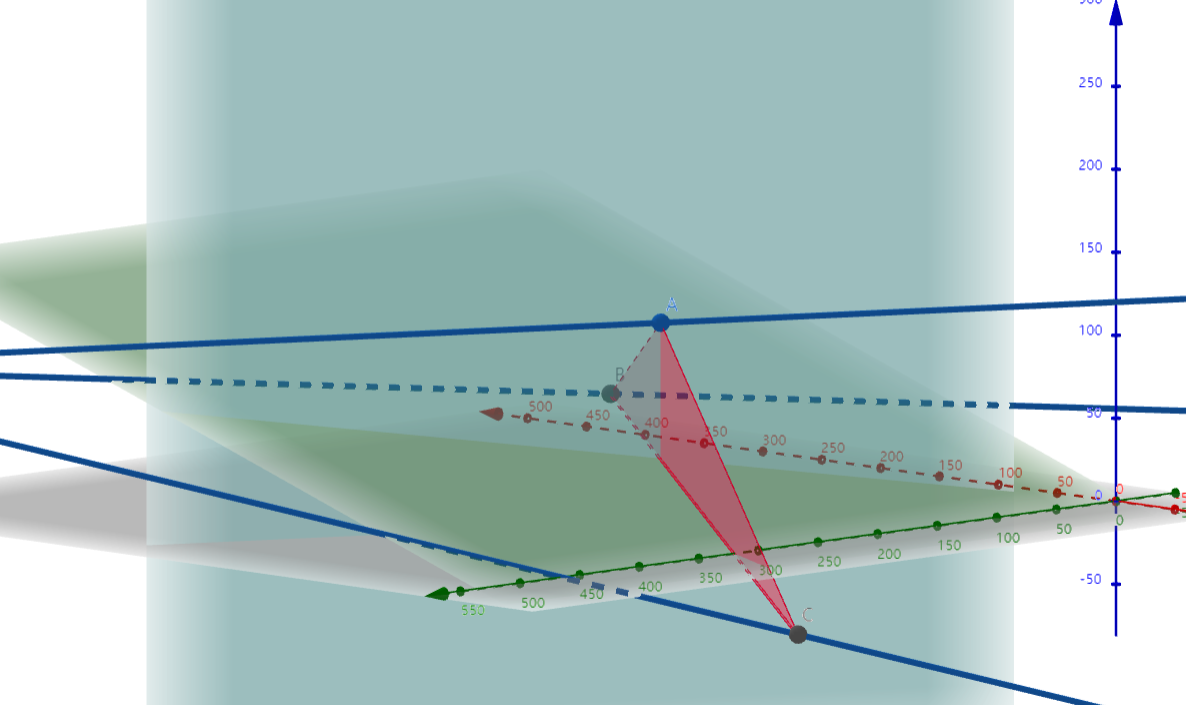
2.第三道题
这道题属于单一变量优化问题，其他条件都不会变，我们只需要讨论测线的角度这一个变量即可。
3.第四道题-初步思路
这道题中，地面不再是平坦的了。
我们知道，我们需要将其转化为之前的条带的形状会比较好计算。
即我们可以求测线左侧和右侧宽度的平均值，然后再对他们进行计算。
需要注意的是，题目给出的数据是离散的，位于格点上的，所以说实际上，我们需要对每一个点取一个近似的位置作为取样点，并且加以运算。
.jpg)
.jpg)
之后我们再在β里面求取使得测线长度最小的值
.jpg)
最后我们需要检验漏测率，这里需要注意的点其实还是数据是离散的
.jpg)
最后可以得到结果大概是117度
4.第四题还可以优化
我们发现，地图中有明显的较为陡峭的部分，也有明显比较平缓的部分，将两者看作是一种显然会造成十分大的误差，那么在这种限制之下，我们可以考虑将整块地分割为四个部分，并且对其进行分别处理。